

Hence, we will create a new node with the same value and return this new node. When we have only one node in the range, then this node is already sorted. Q) What should be the base case of the recursive merge sort function?
Sort linked list how to#
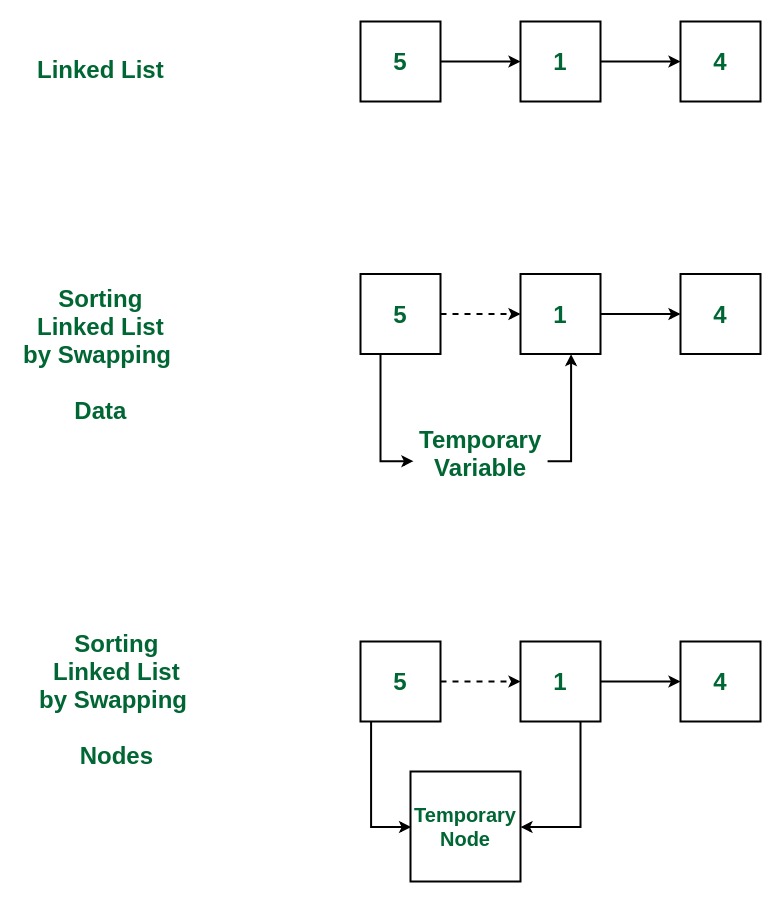
We know how to merge two sorted linked lists, right? I am not going to explain how to write the merge operation, which we wrote earlier.Now, we need to merge these sorted linked lists into a single linked list, which should be sorted as well. We have two linked lists which are in sorted order separately.Q) How to combine the results of smaller subproblems to solve the current larger problem, i.e. On calling mergeSort recursively, we will get two new sorted lists. call mergeSort to sort the left part (from head to mid) and also call mergeSort to sort the right part (from mid->next to tail). We will recursively call for the smaller subproblem, i.e. So, now we know how to find smaller subproblems. We will use the function mid() which we wrote earlier directly. I am not going to explain how to find the middle node of the linked list in this article again.and in every iteration, we set the p variable to the first node of the list and the q variable to the second node of the list. in the first iteration, we set the end variable to None. to sort a linked list first we need three references p, q, and end. like in the example we have a list of 5 items then we need to iterate over the list for 4 times. The Linked List is binary i.e data values in the linked list nodes consist of only 0s and 1s. In a bubble to sort a linked list that has n items, we need to iterate over the list n-1 times. We know how to get the middle node of a linked list in one traversal using the concept of slow and fast pointers, right? Given a Linked List A consisting of N nodes.
In the linked list, to get the middle node of the current range, we will have to do a traversal of the current range, as we cannot get direct access to the middle node.But, in arrays, getting the middle index to split the left & right ranges is easy, as we can randomly access any index in O(1) constant time.Similar to what we did in arrays, we will sort the first half of the linked list and the second half of the linked list separately.Q) How to divide the problem into subproblems? How can we use the concept we learnt there to solve this problem?Īs we know that merge sort is a Divide & Conquer Algorithm, we can solve a larger subproblem by dividing the problem into subproblems recursively, and combining the solved smaller problem to solve the larger problem. We know how to merge-sort an unsorted array. Reverse Linked List (pointer - Recursive) Solution: Usually Merge Sort can used to sort a Random. Remove Duplicates In A Sorted Linked Listĭisplay Reverse (recursive) - Linked List Given a Singly linked list with each node containing either 0, 1 or 2.


 0 kommentar(er)
0 kommentar(er)
